
Physics in the pandemic: ‘There are some great experiments that can be done safely and simply at home’
by Matin DurraniStefan Hutzler and Denis Weaire are in the School of Physics, Trinity College Dublin, Ireland. Their postgraduate student Ali Irannezhad currently performs his experiments in his home in Tehran, Iran. This post is part of a series on how the COVID-19 pandemic is affecting the personal and professional lives of physicists around the world. If you’d like to share your own perspective, please contact us at pwld@ioppublishing.org.
With COVID-19 sending universities and schools into a long summer hibernation, how are we to adapt to our confinement? Teaching and research will probably continue to be a solitary, online affair, as it has for most of the pandemic so far, with many of us cooped up in tiny bedrooms.
Indeed, it will be interesting to see what lasting effect online lecturing has on traditional teaching methods. It’s fair to say we academics have not always been honest with ourselves about the quality of our university lecturing: in the late 1990s, one of us (DW), wrote a humorous “lateral-thoughts” article in Physics World about the horrors of university life, focusing on the torture of the ill-prepared lecturer confronted by a smart student.
But what about experimental physics? Doing simulated experiments on a screen holed up in our bedrooms can surely never be an adequate substitute for the real thing?
However, we think there are some great experiments that can be done safely and simply at home, using materials that are readily at hand. Mostly they relate to classical mechanics or elementary properties of materials. After all, as physicists like Eric Mazur from Harvard University have long argued, classical physics is the best training for rigorous thought, with even apparently trivial experiments throwing up teasing challenges.
Line of action
Consider one experiment we recently wrote about in the American Journal of Physics. Take a convenient number of ball bearings or similar hard spheres. Place them in a tube with stoppers at both ends, lay it horizontally, and then agitate it slightly to encourage the system to equilibriate. (Immersing the balls in oil will help.)
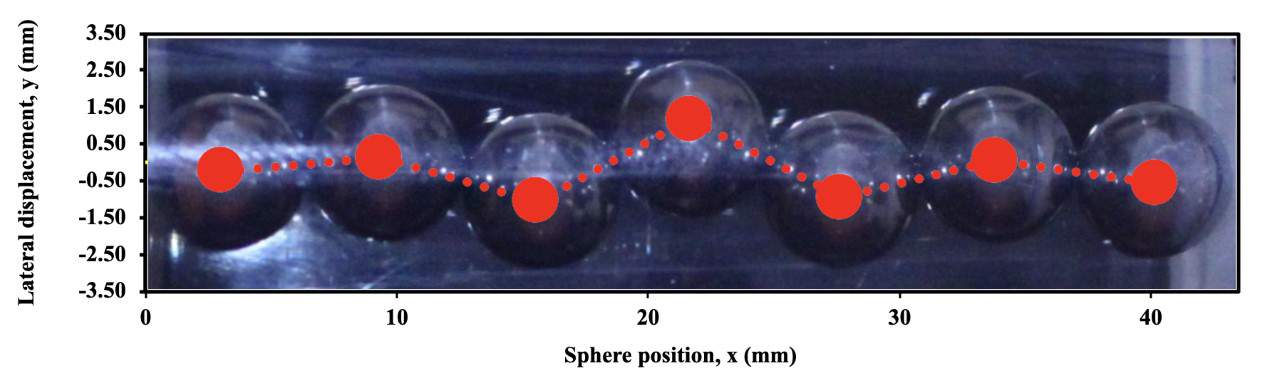
Turns out that if you compress the chain of hard spheres enough by adjusting the stoppers, it buckles (see above). What’s more, the buckling is localized, rather like the “kinks” and “solitons” in many non-linear systems. There’s also an interesting difference depending on whether you use an odd or even number of balls. You could even try using soft bubbles inside of hard spheres.
And having got your data, why not try to replicate your results by computer simulation, perhaps using Python programming? As the great John Von Neumann once said, the computer (which he helped to invent) is supposed to release mathematics from the narrow confines of linear problems.
Cradle of genius
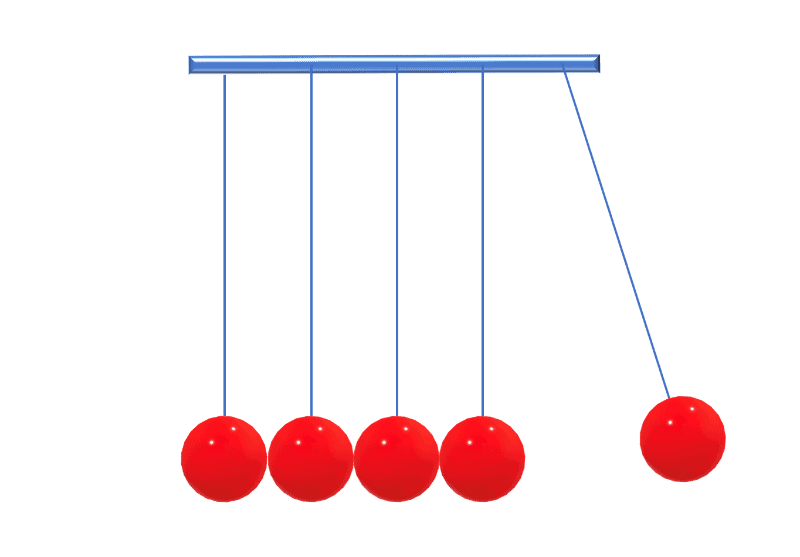
Another hard-sphere experiment is Newton’s cradle, commonly associated with Isaac Newton, who by the way made some of his greatest achievements while isolating in the countryside during the plagues that ravaged Britain in 1665 and 1666. It’s not hard to understand the basic properties of what’s now a classic executive desk toy, but all good scientists will want to look at it more closely. That’s exactly what John Hinch and Sébastien Saint-Jean did in 1999, as we did too five years later in a paper called “Rocking Newton’s cradle”.
In the standard textbook description of Newton’s cradle, only one sphere is ever in motion. However, if you look really carefully, you’ll notice that all spheres can be moving at the same time. Theory and computer simulations confirm this, and attribute it to the finite elastic modulus of the spheres.
Bubbles and borders
What about soap bubbles, brought from the kitchen? Stare into a foam with the naked eye, or with the help of a magnifying glass, and you’ll see local order amongst the chaos. Three soap films, for example, always meet in a line under an angle of 120o, while four such lines meet under the tetrahedral angle of 109.4o. The lines are called Plateau borders in honour of the Belgian scientist Joseph Plateau who was the first to describe them in a series of experiments. Indeed, he may well have done some of them himself at home after blinding himself by rashly staring at the Sun (in the interests of science).
Or rather than grabbing bubbles from the kitchen sink, how about blowing air through a straw into some soapy water? Blowing carefully (or using an aquarium pump borrowed from your fish) results in the generation of bubbles of equal size. These crystallize spontaneously to form a hexagonal pattern (triangular lattice) on top of the soap solution, with some defects, such as dislocations, amongst them.
In 1947 the Nobel-prize-winning physicist Lawrence Bragg and his colleague John Nye studied such a 2D bubble raft at the Cavendish Laboratory, Cambridge, as a source of inspiration for the study of crystalline defects. There wasn’t a plague on, but these two great physicists may have been examining such simple classical physics because the Second World War was only just over and had left even Cambridge University impoverished.
There’s even more entertainment and food for thought from 3D structures formed by monodisperse bubbles, which the photographer Kym Cox recently brought to prominence last year in New Scientist and the New York Times. In fact, it was one of us (SH) who taught her the tricks of how to make these amazing structures in her own kitchen.
Don’t wake the neighbours
Finally, let’s look at the Euler disc, named in honour of the great mathematician Leonhard Euler (though there’s not evidence he originated it). All you need is a simple, flat disc, preferably a heavy one although a large coin will do. Spin it on a firm, flat surface and you’ll notice it gradually subsides, as its energy is dissipated. But instead of a dignified, gradual exponential approach to equilibrium, the coin heads dramatically towards a crisis, emitting a sound of ever increasing frequency. It suddenly settles – not with a whimper but a bang. (If you’re using a really heavy disc, try not to wake the neighbours…)
Our challenge to you is to find a way of measuring this intriguing sound. But if you want the explanation, Keith Moffatt (who like Newton was at Trinity College Cambridge) has written eruditely on the subject in Nature, As a side note, a previous paper of his led one of the present authors (DW), while still an undergraduate, to throw eggs out of his second-story student room on to an adjacent lawn; Moffatt claimed they wouldn’t break, and he was (mostly) right.
Some day soon we’ll all return to our schools and labs, where remarkable and expensive equipment awaits us. When that happy day arrives, perhaps our time at home will have let us bring a deeper appreciation and admiration of the many visual phenomena that are already around us. Those phenomena may look trivial, but they can be challenging, teaching us to speculate and analyse until we get to the heart of the matter. And as so often in physics, simple matters may tempt us to go deeper and deeper still.
Precautionary note: None of our suggestions should pose any significant hazards in the home environment, but we advise you to take all necessary precautions and care while carrying out any experiments